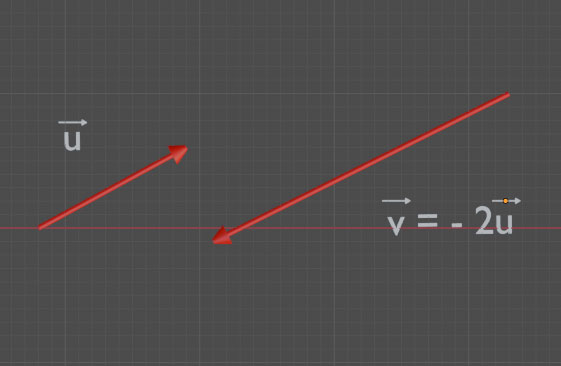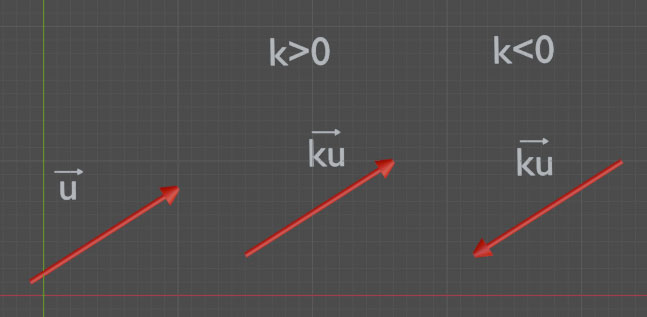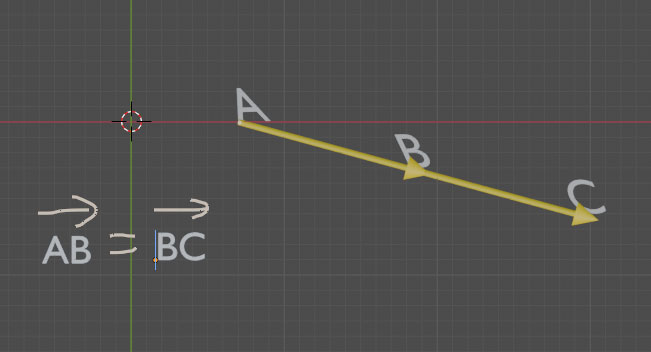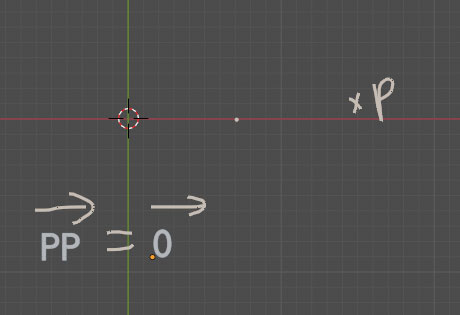Exemple:
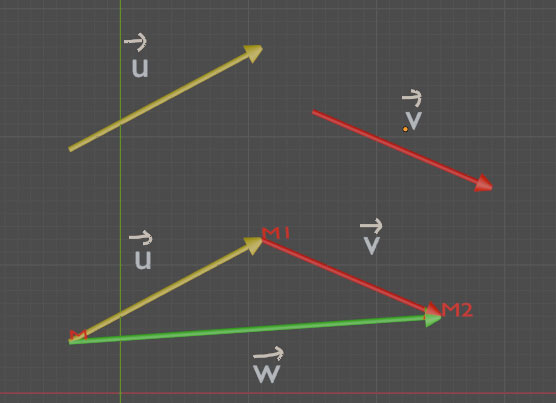
On appelle somme des vecteurs u et v, notée u + v, le vecteur w associé à la translation composée des translations de vecteurs u et v.
Soit t1 la translation de vecteur u et t2 la translation de vecteur v.
Appliquer la translation t1 puis la translation t2 revient à appliquer la translation t de vecteur w.
Deux vecteurs non nuls u et v sont colinéaires signifie qu'ils ont même direction c'est à dire qu'il existe un nombre réel tel que :
=
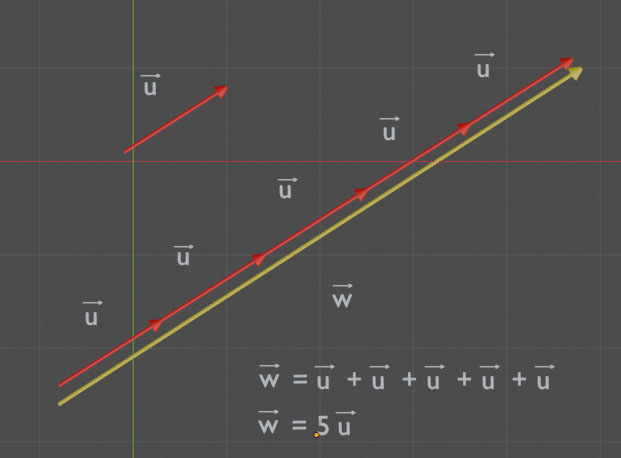
On appelle produit du vecteur u par le réél k, le vecteur noté ku:
- De même direction
- De même sens que u si k>0 et de sens contraire si k<0,
- De norme égale à k fois la somme de u si k>0 et -k fois la norme de u si k<0
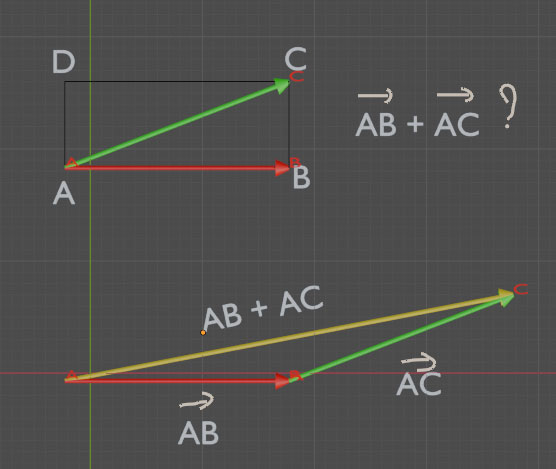
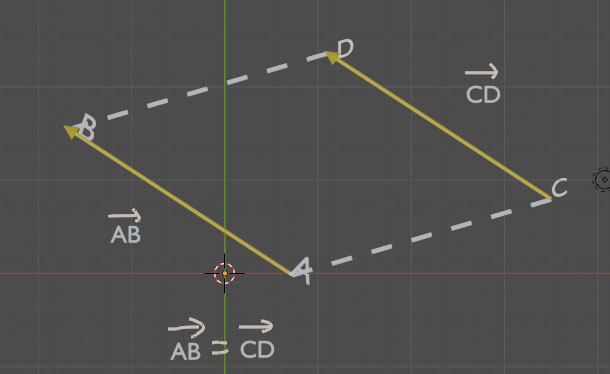
Propriété caractéristique d'un parallélogramme:
Dire que ABCD est un parallélogramme revient à dire que :
+
=
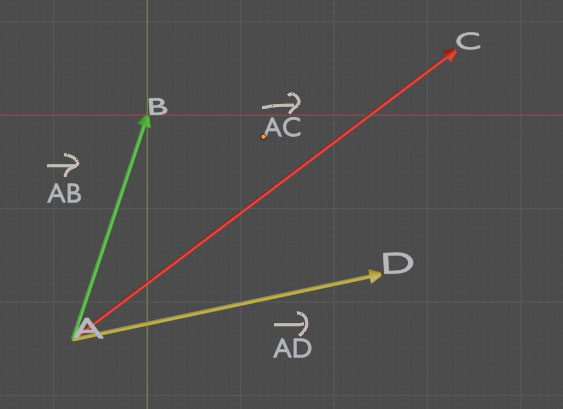
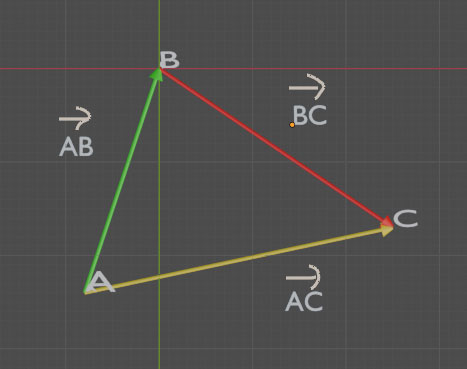
Pour tous points de A, B et C du plan, on a:
+
=
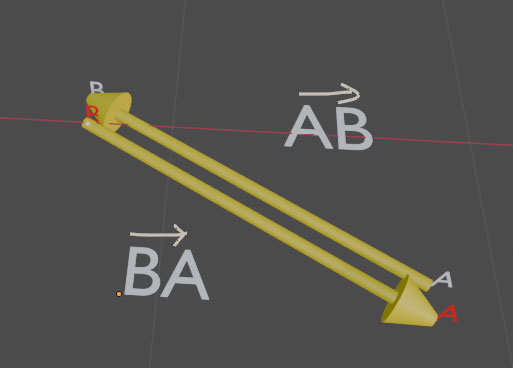
Deux vecteurs sont opposés lorsqu'ils ont la même direction, la même longueur et qu'ils sont de sens contraire.
-
=
Un vecteur est nul lorsque les points A et B
Un vecteur
=
sont confondus.
et
et
Dire que B est milieu du segment [AC] revient à dire que
sont égaux
sont égaux
alors B et le milieu du segment [AC]
La reciproque est vraie: si
et
Les deux vecteurs
ont la même direction, le même sens et la même longueur.
Dire que ces vecteurs sont égaux revient à dire que le quadrialatère ABDC est un parallèlogramme, éventuellement aplati.
Est un représentant du vecteur
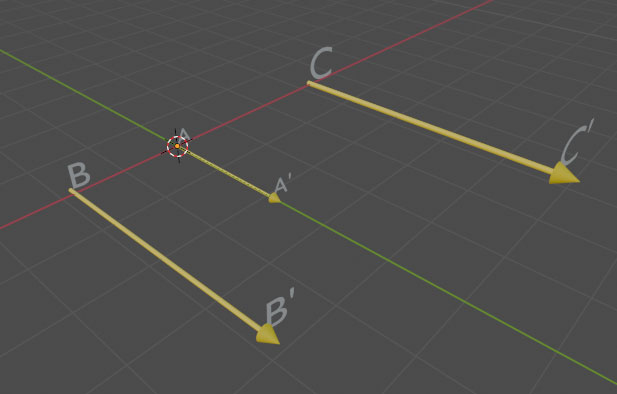
Un vecteur est défini par:
1-Une direction : Celle de la droite (AA')
2-Un sens : de A vers A'
3-Une longueur AA'(norme du vecteur)
- Un vecteur à plusieurs représentation car il n'a pas de position prédéfini sur le plan.
- Un vecteur se représente à l'aide d'une flêche.
- Un vecteur ne dépend pas des points qui l'on construit
- Deux vecteurs sont égaux lorsqu'ils ont même direction, même sens et même longueur.
Voici un rappel des différentes propriétés des vecteurs.
Les vecteurs